Подключил сам CSS фреймворк Bootstrap, подключил библиотеку jQuery (последнюю ве...
Расширения Joomla
Шаблоны Joomla
Комментарии
-
Быстро, просто, легко - Eleano...
SLAED CMS Pro потребляет на сколько мне известно 1... -
Уроки 3D-Max: Объекты на белом...
Здравствуйте, у меня такая же проблема - как тольк... -
Установка ionCube на локальный...
спасибо, добрый человек:))) -
GK Steak House - ресторанный ш...
Если у вас joomla 2.5 то необходимо обновить recap... -
JomSocial 2.2.4 RUS
Как устанавливать то? нет установочного файл
uGuide - рейтинг "Конструктор сайтов" . Инструмент для автоматизации бизнеса и управлением продажами - CRM система Мегаплан
Популярные расширения Joomla!
Компонент - Agora Forum v3.0.142
Самый лучший компонент форума для Joomla. Стабилен в работе, позволяет произвести миграцию с других…
Компонент форума - Kunena 1.7 stable
Вышла новая стабильная версия компонента форума Kunena с полной поддержкой Joomla 1.7.
Компонент форума - Kunena v1.6.2 Rus
Компонент форума, который разработан специально для Joomla 1.5. Устанавливается стандартными…
Компонент - Phoca Guestbook 3.0.0
Компонент гостевой книги для вашего Joomla сайта с защитой от спама. Простая гостевая книга без…
Компонент галереи для Joomla Phoca Gallery RUS
Представляем самую последнюю версию компонента галереи для Joomla Phoca Gallery. Бесплатный…
Модуль - Contact Form FX
Модуль Joomla для создания формы обратной связи на вашем сайте, работает при помощи технологии…
Импорт и экспорт материалов в Joomla j2xml
Сегодня хочу вам представить бесплатный компонент Joomla, который бывает просто незаменим при…
Cost Calculator - калькулятор для Joomla
Cost Calculator - компонент калькулятора для Joomla сайта. Легок в установке и настройке. Позволяет…
Обсуждают на форуме
Здравствуйте! Подскажите пожалуйста, есть ли в Illustrator альтернатива функции ...
При переходе с Joomla 1.5 на 2.5 и 3 возникла проблема с адресами перехода/ссылк...
Хочу сделать интернет-магазин на Joomla + Virtuemart, но вот нашел скрипт Magent...
Нужно написать порядка 40 текстов по 2500 символов на тематику туризма и путешес...
Новинки шаблонов Joomla! и шаблонов Bootstrap
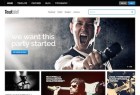
GK Steak House - ресторанный шаблон Joomla
Ресторанный шаблон для Joomla работающий в связке с компонентом K2. Шаблон имеет хороший потенциал среди владельцев…
GK Events - сайт событий и мероприятий на Joomla
20619
Очень неплохой шаблон для создания сайта мероприятий и событий на CMS Joomla 2.5/3.x. Шаблон имеет очень…
GK University - шаблон для образовательных сайтов
20235
Качественный адаптивный шаблон для вузов на CMS Joomla от профессиональной студии дизайна GavickPro. Шаблон имеет 3…
GK Storefront - интернет-магазин на базе VirtueMart
Легкий шаблон на базе Virtuemart и Joomla 2.5/3.2. Шаблон выполнен в минималистичном белом стиле, но в тоже время…
GK John - шаблон для портфолио
18455
Качественная тема для создания личного портфолио в интернете. Шаблон создан на базе Joomla в связке с модулями GK News…
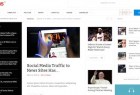
GK News 2 - тема для новостного портала
22314
Вам нравятся новостные сайты наподобие The New York Times, cNet и пр.? Вы можете создать такой-же интернет сайт,…
GK Mo - шаблон для портфолио и призентаций
23073

Классный, стильный шаблон для бизнес сайта или сайта портфолио. С шаблоном под названием "MO" вы можете легко создать…
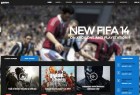
GK Game - шаблон для игрового портала
Тема оформления для Joomla 2.5/3.2+ под названием - Game от студии Gavick. Шаблон предназначен для новостных сайтов с…
GK inStyle - шаблон для интернет магазина Virtuemart
20045
Профессиональная тема оформления для компонента интернет коммерции - Virtuemart. Шаблон совместим с Joomla 2.5/3.2+ и…
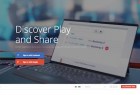
Palette - параллакс шаблон на Bootstrap
Красивый HTML одностраничник (или OnePage) созданный на основе фреймворка Bootstrap 3.1.1. Шаблон имеет поддержку…
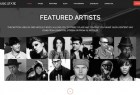
GK Music state - шаблон для музыкального сообщества с поддержкой JomSocial
22809
Стильный шаблон для музыкального портала под названием Music State. Шаблон работает на джумла 2.5/3.2+ и поддерживает…
GK CloudHost - шаблон для хостинг компании
22064
Мощный шаблон для сайта хостинг-компании или интернет-провайдера. Шаблон работает на Joomla 2.5 или Joomla 3.2+ при…
GK M Social - шаблон для социальной сети
20119

Используете CMS Joomla 2.5/3.2+ и компонент JomSocial? Тогда шаблон M Social от разработчиков GavickPro именно то что…
GK Shop and Buy - шаблон с поддержкой Virtuemart
20928
Шаблон для интернет-магазина на базе компонента Virtuemart и CMS Joomla 2.5/3.2+. Шаблон выполнен в стиле минимализма,…
Light Blue 2.0 - шаблон Bootstrap для административной панели
Очень качественная HTML/jQuery тема для административной части сайта. Шаблон разработан на Bootstrap 3.0.0 с…
Articulate - шаблон для портфолио и резюме
Адаптивный HTML шаблон для создания сайта портфолио или резюме. Шаблон построен на фреймворке Bootstrap 3.0.3 и имеет…
DesignR - профессиональный шаблон для портфолио
Очень качественный и профессиональный шаблон одностраничник для создания сайта портфолио. Шаблон выполнен на чистом…
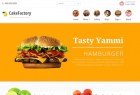
Cake Factory - шаблон Bootstrap для ресторана
23421
Простенький HTML шаблон созданный на базе Bootstrap 3.1.1, HTML5 и CSS3. Хорошо подойдет для создания сайта ресторана…
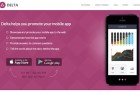
Delta - бизнес шаблон Bootstrap
Очень красивый HTML одностраничник с использованием последней версии фреймворка Bootstrap 3.1.1. Шаблон предназначен…
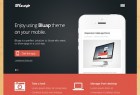
GK Bluap - бизнес шаблон Joomla
21209
Если вы являетесь разработчиком какого либо приложения, компьютерной программы или веб-скрипта, вы легко можете…
GK Creativity - тема для портфолио
23323 1

Неплохой качественный шаблон для Joomla 3/2.5. Шаблон предназначен в большей степени для создания сайтов портфолио,…
GK RockWall - музыкальный шаблон
20033
Шикарный шаблон для создания новостного сайта или музыкального портала на CMS Joomla 2.5 или 3.2. Шаблон выполнен…
JA Appolio - шаблон для портфолио
20431
Красивый шаблон для создания сайта портфолио на CMS Joomla 2.5/3.2. В шаблоне имеется поддержка фреймворка Bootstrap 3,…
JA Obelisk - шаблон для онлайн кинотеатра
21312
Мощный шаблон JA Obelisk подойдет для создания сайта онлайн-кинотеатра. Для отображения кинофильмов в шаблоне имеется…
JA Magz - шаблон для новостного сайта и блога
19132
Один из самых красивых новостных шаблонов для Joomla (2.5/3.2) выполненых в минималистичном стиле. Шаблон был…
JA Muzic - шаблон для сайта развлечений и музыки
21608
Адаптивный шаблон для CMS Joomla 2.5/3.2 с поддержкой компонента блогов EasyBlog и нового расширения JA AV Tracklist с…
JA Fixel - интерактивный шаблон Joomla
19843
Качественный интерактивный шаблон Joomla от мега студии Joomlart. Шаблон имеет множество стилей оформления, как в…
JA Beranis - бизнес шаблон для сайта
19282
Современный бизнес шаблон для сайта под управлением Joomla 3.2 и Joomla 2.5. Шаблон построен на фреймворке T3 (студии…
JA Smashboard - шаблон для сайта развлечений
18840
Шаблон Joomla 3.x и Joomla 2.5.x для создания сайта развлекательной тематики. На шаблоне можно создать красивый сайт…
JA Hawkstore - шаблон интернет магазина
20903
Мощный шаблон для Joomla CMS от разработчиков студии Joomlart. В шаблоне имеется 100% поддержка компонента Virtuemart,…
Новинки расширений Joomla!
Компонент ZOO Pro RUS v 2.4.9
43295 2

Компонент ZOO от известных разработчиков yootheme предназначен для структурирования контента на Вашем Joomla сайте.…
Компонент K2 RUS
33864
Популярный компонент для создания материалов на вашем Joomla сайте в виде блога или каталога. О компоненте K2 говорить…
Columnist
24674

Компонент Columnist предназначен для продвинутого управления материалами вашего Joomla сайта. При помощи этого…
Модуль JUNewsUltra Pro
28932
Модуль для Joomla 1.5-3.0, служащий для вывода материалов на Вашем Joomla сайте. Модуль многофункциональный и…
ContentBuilder
Быстрый и мощный компонент ContentBuilder создан для того, чтобы помочь вам структурировать ваш контент на Joomla…
OSContent
22310
Компонент для Joomla 2.5, предназначенный для управления материалами, разделами и категориями Вашего Joomla сайта.…
User Article Manager
23278
Компонент для Joomla 1.7/2.5 который позволяет администратору и пользователям, находящимся в группе "Авторы" создавать…
Daily Aphorism
22278

Модуль для Joomla 1.5-1.7, который выводит на страницах Вашего Joomla сайта афоризмы, стихи, анекдоты, выдержки или…
Новинки сниппетов Bootstrap
Увеличительное стекло на изображении с помощью Bootstrap
Мая 12, 2014 21901
Классный JS эффект "лупы" с помощью фреймворка Bootstrap 3.1.1. Если у вас на сайте есть большие фотографии и вы хотите…
Профиль пользователя сайта на Bootstrap 3
Мая 07, 2014 28017 2

Очень красивая страница для профиля пользователей вашего сайта с применением Bootstrap 3.x. Страница имеет очень…
Лайтбокс эффект с применением Bootstrap
Апреля 10, 2014 20254
Простая реализация всплывающего окна на фреймворке Bootstrap 3.1.1. Минимальное количество кода и прекрасный внешний…
Простая форма авторизации на сайте с Bootstrap
Красивая форма авторизации на сайте с применением фреймворка Boostrap 3.1.1. Очень простая реализация с минимальным…
|
|||